Pair-wise sequence alignment methods part II
Outline: a Generalized algorithmic approach for global sequence alignment
To run the global sequence alignment algorithm in a computer, we need to consider the following components:
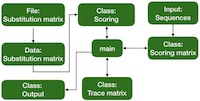
1. The scoring matrix. The scoring matrix stores all the results of each character by character alignment calculation.
2. The scoring function. The scoring function calculates the highest value of match or mismatch and gap.
3. Substitution matrix. The substitution matrix contains values for each nucleotide or amino acid substitution. An alignment program usually loads a chosen substitution matrix at the start.
4. The trace matrix. The trace matrix. The trace matrix stores the decision of highest scoring choice for each character pairing, given by the scoring function.
Figure 1 outlines one possible program design. This design is only one of many possible ones, and although it is clear, it isn't the fastest running one.
1. Scoring matrix
In a computer, we need a structure to store our calculations. We call this structure a scoring matrix, and we put both sequences s1 and s2 into the first row and column respectively. After which we precalculate the gap scores at the beginning of both sequences and put them into the matrix as well. In case we insert gaps at the beginning, the s1 looks like this:
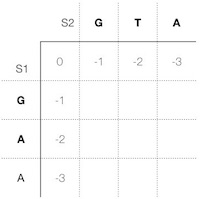
(1 gap: -1) _GAA,
(2 gaps: -2) _ _GAA,
(3 gaps: -3) _ _ _ GAA.
Analogously s2 looks like this:
(0 gaps: 0) GTA
(1 gap: -1) _GTA,
(2 gaps: -2) _ _GTA,
(3 gaps: -3) _ _ _ GTA.
We need the beginning gap scores only at the first row and column. When inserting gaps to s1, the gap scores are to the left, and gap scores for s2 are at the top. In all other rows and columns, we use the previous highest score in the cell to the left and at the top of a current cell for a gap in s1 and s2 respectively (Figure 2).
It is an excellent practice to pre-calculate the beginning gap scores and store them directly in the scoring matrix. This way, the system doesn't need to calculate the scores every time.
The scoring matrix may be a separate class, e.g., "ScoringMatrix" (Figure 1) and contain public functions for loading the sequences from a file, pre-calculating the beginning gap scores, returning cell scores, setting a value of a cell, and so on.
2. Scoring function
Before we can make any calculations, we need to decide how to score matches, mismatches, and gaps; thus we create a scoring function. Having a single function which calculates the scores the same way in each cell of the matrix is an advantage.
In this case we use a simple scoring system as follows:
match score (m) = +1,
mismatch score (mm) = -1,
and gap score (g) = -1.
Our scoring function S is
S = Max(c1, c2, sl1, sl2, d) Where c1 is a current character of s1, c2 a current character of s2, sl1 a previous score to the left of a current cell, sl2 a score on the top of a current cell, and d is the score diagonally up to the left of a current cell.
In this possible design, the scoring function resides in a class "Scoring," which handles the substitution matrix data. At the start of the program "Scoring" loads the substitution matrix data.
In the main loop, we use the ScoringMatrix functions and fetch c1, c2, sl1, sl2, d, and pass to the public scoring function in the class "Scoring," which returns the score for the current cell. This score is stored into the "scoringMatrix" by its public function.
This operation requires a double for-loop in the main and its dimensions are sequence length s1 (n) times sequence length s2 (m). In other words, the running time of the program grows quadratically with increasing length of the sequences. For this, the computer science notation is O(nm) so-called big O notation. To say it in another way, the number of principal operations for two sequences of length 10 is 10x10=100, and for the lengths 100, the number of operations is 100x100=10,000.
3. First calculation
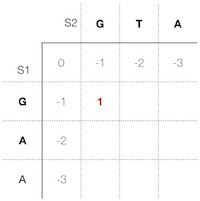
To begin with, we consider the alternative alignment possibilities in the first position. They are
1. Match G with G, in this case we need to add the previously calculated match score located diagonally up left (prev-d).
2. Make a gap in s1, then the precalculated gap (pre-g) cost is -1.
3. Make a gap in s2 with precalculated gap cost of -1.
They correspond to the following alignments:
1. G : prev-d 0 + m = +1 G 2. _ G: pre-g -1 and g -1 = -2 G 3. G : pre-g -1 and g -1 = -2 _ GIn our design, we pass the following data from "scoringMatrix" to the public scoring function in the class "Scoring:" the characters of s1, s2 reflecting the current position, and the three previous scores sl1, sl2 and d.
The scoring function returns the best score for the alternative 1; thus, we store 1 into the current cell using the public function in the class "ScoringMatrix" (Figure 3).
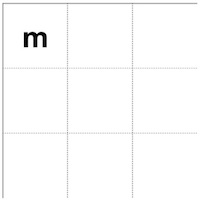
4. Trace matrix
Here we store the information about how we got the highest score in each cell because we need the data later when constructing the sequence alignment for output.
In the first calculation, we got +1 by matching G from s1 and G from s2. So, we put "m," meaning match in the first cell.
Also, "m" means that the previous value for this calculation came from the previous cell located diagonally up left.
This design has a separate class, "Trace_matrix," which contains the matrix itself plus public functions to store and retrieve values (Figure 4). Note that the scoring function must return in addition to the score itself, the type of the best score, i.e., one of the alternatives 1, 2 or 3 so that the program knows what to store into the trace matrix.
5. Cell no. 2
The next step is to calculate the score in the cell no. 2. Again, we have three possibilities: (1) make a mismatch in which case we need to add the previous diagonal score up left, -1, (2) make a gap in the sequence s1 and to add the score in the cell to left of the current cell, +1, or (3) lastly we can make a gap in the sequence s2 and add the score in the top cell -2.
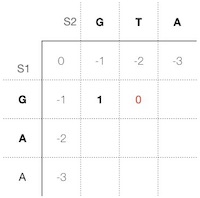
1. T : prev-d -1 + mm -1 = -2 G 2. _ T: pre-g1 +1 + g1 -1 = 0 G 3. T : pre-g2 -2 and g2 -1 = -3 _ GOur scoring function gives the best sore for alternative 2; thus, we put 0 in the second cell of the scoring matrix (Figure 5). In the next step (6), we store the type of the operation into the corresponding cell of the trace matrix.
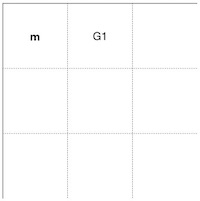
6. 2nd cell trace matrix
Time to store the way how we got the highest score in the scoring matrix cell no 2. Since we got it by making a gap in the sequence s1, we mark it as "G1" in the trace matrix (Figure 6).
It also means that the previous highest value is to the left in the previous cell on the same row. This information is valuable when we construct the whole alignment by tracing these operations backward starting from the bottom rightmost cell.
7. Filling the rest of the scoring matrix
We continue to calculate each cell in the scoring matrix the same way and store the way how we got the highest score in each cell in the trace matrix until we reach the last cell (Figure 7 and Figure 8).
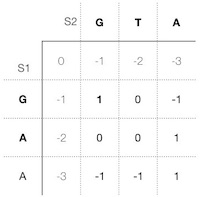
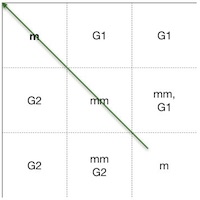
Since we only need to keep track of the three previous values to the left of the current cell, i.e., the last diagonal cell score (match or mismatch), the left cell score (previous gap on s1), and top cell score (previous gap on s2), we can do all the calculations either row by row or column by column. The result will be the same in either of the cases.
Once we have calculated the last cell on the last row and column, we have finished the scoring matrix. The score in this last cell is the same as the alignment score.
The last thing we still need to do is to construct the alignment itself, by following the cells backward in the trace matrix. We do this by starting from the bottom rightmost cell and follow backward the alternatives by which way we got the final score and stop at the first cell on row 1, column 1. The green arrow marks the path (Figure 8).
In this simple example, we only got a single best scoring alignment alternative
GTA
GAA
with two matches and one mismatch, and the total alignment score of +1.
In fact, in long sequence alignments there can be tens of thousands of equally good sequence alignments and it is up to the programmer to decide which one to present to the user. The general user is often unaware of this, because of most of the pair-wise sequence alignment programs don't include the information of how a software program prioritizes equally good alignments.
Regardless of which scoring system we use, pair-wise sequence alignments do not contain enough information to make a difference between identically scoring alignments. To gather additional information, we need to compare multiple sequences, but that is the topic in multiple sequence alignment tutorial. For now, the next step is to explore pair-wise local alignments.
Take a look at the online Dynamic Programming implementation of global sequence alignments. The program aligns two DNA sequences and has an extra feature, affine gap penalties, in the "More parameters section."
The idea of affine gap penalties is to minimize the number of gaps in an alignment. In this sense, a gap count is not character by character but can span several characters and is still considered one gap. In the affine approach opening of a gap is penalized higher than extending an existing gap, reducing the number of short gaps. Other gap penalty types are linear, convex and profile based.
You may also like:
Homologs
or homologous sequences
Sequences that have a common ancestor.
Substitution
A mismatch in a sequence alignment.
Indel
Stands for insertion or deletion.
Gap
One or several consecutive indels.
Substitution matrix
Also 'scoring matrix'. Used for assigning substitution scores in sequence alignments.
Codon
DNA codes for protein using words of three nucleotides, codons. Each codon codes for one amino acid.
