Bioinformatics tutorial: Pair-wise sequence alignment methods 2022
Learning objectives:
- Gain a basic understanding of Dynamic Programming method for sequence alignment.
- Able to implement a pair-wise global sequence alignment algorithm (Needleman-Wunch).
- Able to implement a local sequence alignment algorithm (Smith-Waterman).
Introduction
Although we could construct very short and similar sequence alignments by hand, there is no point to do this, since many sequence alignment software tools are available. This tutorial describes the core pair-wise sequence alignment algorithms, consisting of two categories: (1) Global sequence alignments algorithms and (2) Local sequence alignment algorithms.
The first part of this tutorial describes accurate methods, and in the second part, we go through the heuristic approaches of the global and local sequence alignments. Loosely speaking, heuristics means a best guess. Heuristic methods have become necessary, already a long time ago, due to the humongous amount of sequences scientists must handle.
How to find the best alignment between two sequences? To efficiently solve problems, we usually break a large problem into smaller sub-problems. We use the same approach here. In general, to choose the best among a collection of things, we need to compare all of them, and only then we can determine which one is the best of all within the group according to some standard.
Therefore, to be able to choose the best sequence alignment among all possible ones, first, we need to list all possible sequence alignments. Only after that, it is possible to compare all of them and consequently choose the best. However, which one is the best, is determined by a scoring scheme and does not necessarily reflect biological relevance. This tutorial only briefly touches this topic, but you can find an in-depth discussion of this in the related tutorials sub-section below.

Consequently, the next question is how many different sequence alignments can there be between two sequences? Well, it depends on the sequence length and the number of gaps we allow. To begin with, we need to limit their quantity and make a rule that they are not allowed to be in the same position on both of the sequences because the alignments would become infinitely long. Anyway, such sequence alignments would not make sense (Figure 1). Given this constraint, how many different alignments can we then make?
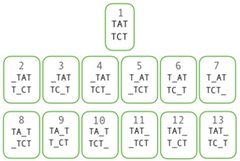
Let's make a test with two short sequences of length three. If we don't allow gaps, there is only one possible alignment, since the sequences are the same length. If we permit one gap, there are 12 possible different alignments, given the constraint that no gaps are allowed to be in the same position on both of the sequences. Let's see why. If we insert a gap in the first sequence, there are four different ways we can do that and consequently only three possible positions we can add a gap in the second sequence without making the gaps overlap. Thus, resulting in four times three gapped alignments plus one without gaps, yielding a total of 13 possible sequence alignments (Figure 2).
By following the same logic and allowing precisely two gaps in the first sequence, making it five characters long, we can insert the two gaps in ten different ways, ( 25) = 10. In each of these ten cases, we can add a gap in the second sequence in three different ways. That is, we want to combine two of them; thus, there are three possible ways to do this ( 23) = 3; therefore, we will end up with 30 different alignments (10x3=30).
Similarly, if we insert three gaps in the first sequence, we will have 20 additional alignments. So, the total number of possible alignments of sequences of length three with up to three gaps is 63 (13+30+20=63). Note that we cannot add more than three gaps, because it would result in having only gap characters in the same position on both of the sequences and that is not permitted.
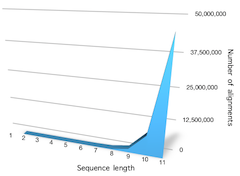
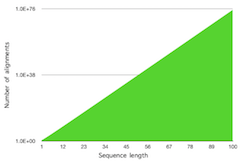
Figure 4. The number of possible alignments of sequences up to the length of 100. Both sequences are the same size. Scale is logarithmic. [Click on the image to toggle zoom ◱ ]
The number of possible sequence alignments increases rapidly with increasing sequence lengths. Two sequences of length 11 have about 45 million possible alignments, and when we grow the length to 134 characters, the number of possible alignments is enormous, about 19x10100. Yes, there are 100 zeros after the number, and it is a googol! Figure 3 shows the number of possible alignments up to the length 11 and Figure 4 shows the number of possible alignments up to 100. Sequences we usually align are much longer than this. For this reason, it is not only impractical but impossible to enumerate all possible alignments; thus, we need to look for smarter algorithms. We explore these in the rest of the tutorial.
Here is a small program that calculates the number of possible sequence alignments for lengths up to 1,000.
Global sequence alignments
Global sequence alignments are alignments where we align both sequences from start to end. In general, the global approach works best when both sequences are approximately the same length. The local approach may produce alignments entirely containing both sequences, but more about that in the next subsection.
How to go about developing the algorithm? Let's use the approach to break a big problem in smaller sub-problems and consider alignments of one character at a time and then use that information to construct the whole alignment. We use the sequences (s1) GATA and (s2) GATTA and the following simple scoring system: match score = +1, mismatch = -1, and gap = -1.
The following approach describes how to test all possible alignments between s1 and s2. Note that at each character position, we can choose to make (1) a mismatch, (2) a gap in sequence s1, or (3) a gap in s2; thus, we only have three choices at each position.
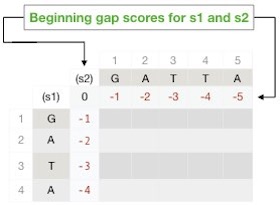
Before we start the calculations, we make a matrix and put sequence s1 in the first column and s2 in the first row. Then we precompute the gap scores for the column zero from 0 to -5, corresponding to the following positions of s2:
(0) GATTA,
(-1) _ GATTA,
(-2) _ _ GATTA,
(-3) _ _ _ GATTA,
(-4) _ _ _ _ GATTA,
(-5) _ _ _ _ _ GATTA,
and for the sequence s1 correspondingly. Note that we cannot add more than four beginning gaps to the s2 since s1 is only four characters long. By pre-computing the beginning gaps, there is no need to compute them each time we need them (Figure 5).
Let's concentrate on the first cell, row 1, column 1. To start with we can make a match G from s1 with G from s2, yielding the match score +1, and since there are no gaps in the front, the total score for the match is 0+1=1 for the alignment of the two characters. The zero score is also in the cell diagonally top left. The next two possibilities are to either insert a gap in s1 or s2. In case, we enter a gap in s1, corresponding to the alignment _ - G, the score is the precomputed gap score -1 plus the gap penalty of -1, giving the total score of -2. THe precomputed gap score is in the left column. The last possibility is to insert a gap to sequence s2, which provides us the total score of -2 also (-1-1=-2). This time the precomputed gap score is in the top cell.
Now, we have tried all possible alignment alternatives for the two first characters of both sequences, and the first cell is complete. That was easy, wasn't it? (Figure 6).
The next step is to proceed to row one and column two or row two and column one. It is a matter of choice. This time, we choose to continue row-wise and compute the row one and column two next.
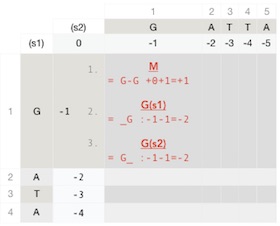
This time we try the pairing A from sequence s2 and G from s1, so this results in a mismatch. The way to calculate the mismatch score is to think that we move the first character G of s1 one step to the right to the position of A of s2. In other words, we added a gap at the front of s1.
The addition of the beginning gap demands that we add the gap penalty to the calculation of the mismatch score. Where do we get this gap penalty?
The beginning gap penalties for s1 are pre-calculated on the row below the s2 sequence, and since this is the first beginning gap, we find it diagonally up to the left of our current cell, which has the value -1. So the mismatch score is gap penalty -1 + mismatch penalty -1 = -1-1=-2 (Figure 7).
Two more alternatives remain, (1) try to pair a gap with A from s2 and (2) G from s1. If we add a gap into sequence s1 at this position, the gap score is as follows. The best previous pairing was the match G-G; thus, we keep G of s1 in its place to the left, and we add one gap after, resulting in the following pairing:
(s1) G _(s2) GSince we already calculated the score for the G-G match, we don't need to compute it again. The resulting gap score is therefore previous best score on the left, in this case, a match +1 plus the gap penalty -1 = +1-1=0.
How about if we add a gap to s2? The meaning of adding a gap to s2 is to add beginning gaps because this is the pairing with the first character of sequence s1 but at the second position of the sequence s2. Adding a gap here means that we are in fact adding two gaps to the beginning of s2 as follows:
(s1) G(s2) _ _ GPlease observe that now we don't have the G-G pairing. The gap score for s2 is then the addition of two gaps -2 plus the gap penalty -1 = -2-1=-3. You can find the gap penalty for the two beginning gaps for s2 conveniently directly at the top of the current cell (Figure 7).
The remaining cells on the first row get their respective scores essentially the same way as in the second cell, which we just calculated. Therefore, we skip the rest of the first row and jump to the second row for the completeness of the description.
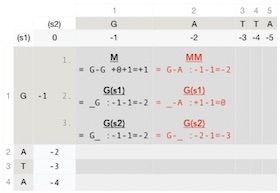
In the second row first column, the characters mismatch (Figure 8). Because the A is the second character of s1 and the first character of s2, we need to account for the gap again in the sequence s2, i.e., we have the following pairing:
(s2) _ G(s1) AThus the score is gap penalty -1 plus mismatch penalty -1 = -1-1=-2. The pre-calculated gap penalty is located diagonally at the top. The value is -1 because this is the first beginning gap.
The insertion of a gap in the sequence s1 means the following alignment:
(s2) _ _ G (s1) G AIt takes two gaps to the front of s2 to bring the A to the gap position; therefore, we account for that. The pre-calculated gap penalty is to the left of this cell with the value of -2 (2x-1), and the score is pre-calculated beginning gap penalty -2 plus gap penalty -1 = -2-1 = -3.
The insertion of a gap in s2 means the following alignment:
(s2) G _ (s1) G ASince this is not the beginning gap, there are no pre-calculated gap penalties. However, the alignment preserves the previous match "G-G"; therefore, we account for that. The score becomes from adding previous match score +1 (top cell) plus gap penalty -1 = +1-1=0.
Now we are finished with the cell and can continue to the second cell on row two.
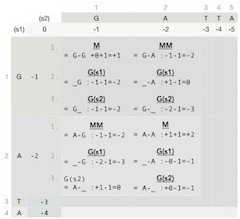
This time we have a match "A-A," and the alignment we are scoring is
(s2) G A(s1) G AIn this case, it is immediately clear that the score should be +2 since our match score is +1. However, it is not so clear further down the road, and that is why we describe the technique that applies to every cell in the matrix.
The score for the previous match is in the cell diagonally up left with the value of +1. Note that in this case, it is a match but if we had previously determined that the insertion of a gap would yield a higher score in that cell, we would have taken that. In other words, we always choose the highest score diagonally up left when we compute match or mismatch.
Consequently, the score for this match is previous match +1 plus current match +1 = +1+1 = +2.
Insertion of a gap in sequence s1 involves the following alignment:
(s2) _ A(s1) A _Also, in this case, we preserve the previous best score, highest out of -2, -3, and 0, given by insertion of a gap in s2. The score is, therefore, the last best score on the row 0 plus the current gap penalty -1 = 0-1=-1.
The last operation in this cell is to calculate the score for insertion of a gap in sequence s2, meaning the following alignment:
(s2) _ _ A(s1) _ AWhat is the previous score we need to add to our computation? It is the best score we previously calculated for s2 in this position. We find it by looking at the best score in the cell directly on the top of this cell. We see the best alignment variant was to insert a gap in s1, giving the score of zero. So, we take this into the calculation, and the score is the previous best score for s2 0 plus current gap penalty -1 = 0-1=-1.
With this, we have completed all three calculations in this cell. All the cells in the matrix use the same approach; thus, we skip the monotonous repetition and look at the final result in Figure 9.
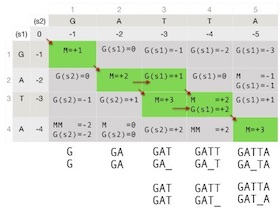
Figure 9 shows the scoring matrix filled. Each cell contains the highest score and the way how we obtained it, i.e., match, mismatch, gap in s1 or gap in s2. The final score, which always is the last one to be computed contains the final alignment score, this time with our scoring system it is +3.
Starting from the rightmost bottom cell where the final score is, we can trace backward to construct the sequence alignment itself. We do this by following the notation of what was the basis to obtain the highest score in each cell, i.e., each prior alignment variant. In Figure 9, also the red arrows show what the basis for each next alignment was. In an attempt to simplify the figure only the arrows involved in the final alignment are present.
In the cell 3, 4 are two ways to obtain the same highest score of +2, one by matching "T-T" and the other by inserting a gap into sequence s1. Therefore, the final two different sequence alignments have the same score of +3. They are
GATTA and GATTA GA_TA GAT_AOn the other hand, pair-wise alignments do not contain enough information to make make a distinction between these sequence alignments having the same score. As mentioned earlier, multiple sequence alignments include more information.
In this example, we tried all possible allowed alignments by solving small subproblems one at the time and building the complete alignment from them.
If you followed and understood the explanation, you now know how Dynamic Programming works or DP for short. A mathematician Richard Bellman invented the algorithm in the 1950s and named it Dynamic Programming for the reason that he wanted even politicians to be impressed of the name. So, the name is a bit scary, but we don't mind, at least I hope so.
Initially, Bellman developed DP as an optimization technique as well as a general computer programming method, and it contains a lot more mathematics than this tutorial, but we skipped all that because it is beside the primary objective here. In 1970, Saul B. Needleman and Christian D. Wunsch published an adaptation of Bellman's algorithm for alignment of protein and DNA sequences. Their version aligns a pair of sequences from start to end; hence, the name global alignment method and also named Needleman-Wunch algorithm.
The above description of the global alignment method would not run efficiently on a computer. We need to adjust it algorithmically and determine an efficient way to use memory. In the next page, we outline one generalized approach, again with no mathematics shorter sequences than above to simplify and bring the essence out.
You may also like:
Homologs
or homologous sequences
Sequences that have a common ancestor.
Substitution
A mismatch in a sequence alignment.
Indel
Stands for insertion or deletion.
Gap
One or several consecutive indels.
Substitution matrix
Also 'scoring matrix'. Used for assigning substitution scores in sequence alignments.
Codon
DNA codes for protein using words of three nucleotides, codons. Each codon codes for one amino acid.
