Pair-wise sequence alignment methods part III
Local sequence alignment
Depending on the scoring system and the similarity of the sequences, the local alignment algorithm may produce a global sequence alignment.
The procedure to create a local sequence alignment is in its core the same as in the construction of global alignments. The main differences are in the initiation of the scoring matrix and construction of the best scoring alignment in the traceback matrix.
Let's start with the initiation of the scoring matrix. Instead of initiating with multiple gap scores, the local alignment matrix initiation is all zeros, so that beginning gaps don't receive any penalty. This way, it is possible to start and stop alignments locally so to speak, i.e., detect high scoring alignment stretches along the sequences without the beginning gap negative scores sinking a local alignment value (Figure 1).
The second difference in local alignment v.s. global alignment is that in local alignment computation all negative values are set to zero. Consequently, if the evaluation of the three alternative alignments (1) match/mismatch, (2) a gap in sequence 1, and (3) a gap in sequence2 would result in a negative value, the scoring function is set to return zero instead of a negative value.
This way, alignment stretches end in zero, and we can locate them by identifying a positive number stretches starting with zero and ending in zero or a set score threshold value.
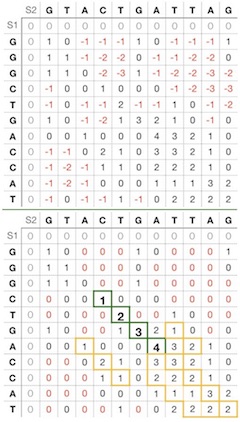
In Figure 2 top the values are calculated in the same way as in global alignment apart from the beginning gap score set to zero. There are a lot of negative scores, and it is difficult to detect high scoring segments.
Compare with Figure 2 bottom, where all negative scores instead are zero. Now it is easy to recognize local alignments that start with zero and end in zero or cut off by a score threshold.
That brings us to the third difference, which is how to find the highest scoring local alignment. We do this by locating all the stretches ending in zero or set threshold value in the scoring matrix. This score is the score of each local alignment.
The traceback procedure is the same as in the global sequence alignment algorithm with the exception that in the local version, the traceback starts from the highest scoring cell(s) or cells that reach up to a set threshold value and ends when the algorithm encounters a zero, this being the start of an alignment segment.
In this example, we have set the score threshold to four, see the alignment in Figure 2 bottom with the green border. This alignment could have continued until the last cell without a set threshold. With the set cut off value, this yields the following local alignment with the alignment score of four:
G T A C T G A T T A G | | | | . . . C T G A . . . .There are four more local alignments, but none of these have a score at least the threshold value of four (Figure 2 bottom).
Ordinarily, local sequence alignment programs report all highest scoring alignments having a score over some threshold in contrary to the global alignment software, if you remember it mentioned in the previous section.
The local sequence alignment method published by Temple F. Smith and Michael S. Waterman in 1981, is also a Dynamic Programming algorithm as the global alignment algorithm. Moreover, guaranteed to find an optimal alignment dictated by a scoring scheme used. The local alignment method also goes by the name Smith-Waterman algorithm reflecting the creators' names.
Heuristic approaches to pair-wise sequence alignment
When handling a large number of sequences, Dynamic Programming algorithms are too slow to be practical. For example, Genbank, a DNA sequence database, on June 15th 2018 release contains 263,957,884,539 bases. That is about 264 billion. If we were to use a Dynamic Programming algorithm to search the database with a sequence length of 1,000 bases, the algorithm is required to make 263,957,884,539 x 1,000 comparisons, which is in total 263,957,884,539,000, i.e., about 264 trillion comparisons. Try to relate the number to processor speed, and you'll find that the comparisons take a long time. That is for a single sequence. Besides that, many people are simultaneously searching the same database.
For this reason, researchers have developed many approaches to reduce the amount of computation required. These methods don't perform all comparisons, but instead, try to predict which sequence pairs might yield an alignment with at least a set threshold score. The approaches are heuristic meaning an educated guess.
The most famous heuristic method is the BLAST algorithm, used for searching similar sequences in databases. A search effectively involves a comparison of all sequences in a database with a search sequence. It works by first creating a dictionary of all the words of set length in a database. This length for protein sequences usually is at least three and for DNA longer, since DNA only consists of four character v.s. 20 in a protein sequence.
The dictionary lookup is a rapid procedure, so BLAST first identifies all overlapping words that are present in a search sequence and contained in the sequence database. Then places the words in a dynamic programming scoring matrix and tries to extend each word to a length that results in at least a threshold score. This way, BLAST only aligns sequences that have enough same common word matches, saving a considerable amount of processing time.
A set number and length of the shared words between sequences yields a probability of two sequences having an alignment with at least a threshold score. Defining the length and number of required common words involves advanced statistics and more about that in the "How does BLAST work?" tutorial.
Key Points
♦ It is not feasible by brute force to try all possible sequence alignments of long sequences. Dynamic Programming solves this by eliminating equal subsolutions.
♦ Dynamic Programming works by breaking a massive problem into smaller subproblems, then solving each of them and compile the solutions to solve the original problem.
♦ In a pair-wise sequence alignment, DP works at character level by evaluating three subproblems: (1) match or mismatch, (2) gap in sequence (a), and (3) gap in sequence (b). Consequently, in the DP matrix, the algorithm only needs three of the previous values to compute a current cell. Moreover, the calculations can proceed either row by row alternatively column by column.
♦ There can be tens of thousands of sequence alignments with the same score. Consequently, to output a single alignment, an algorithm must prioritize one of the three equal scoring alternatives: (1) match, (2) mismatch, and (3) gaps in the traceback.
♦ A sequence pair does not contain enough information to distinguish the best of all equally scoring alignments.
♦ Global sequence alignments are good for alignment of highly similar and equal sized sequences.
♦ Local sequence alignment methods are useful for finding short similar sequence stretches between sequences of varied sizes. Moreover, local alignment algorithms may produce global alignments if sequences are very similar and equal length.
♦ Both global and local sequence alignment algorithms require four components: (1) a scoring matrix, (2) a scoring function, (3) a substitution matrix, and (4) a trace matrix.
♦ To produce a global alignment, initiate the scoring matrix by multiples of gap scores and to produce a local alignment, initiate the scoring matrix by zeros.
♦ Exact alignment methods are too slow for alignment of massive amounts of sequences available today. Heuristic algorithms are much faster but are not guaranteed to find the optimal alignment.
♦ A scoring system dictates an optimal alignment.
What next?
Multiple sequence alignmentRelated tutorials
Introduction to sequence comparison
Pair-wise sequence alignment
Construction of substitution matrices
How to select the right substitution matrix?
References and further reading
Needleman, Saul B. & Wunsch, Christian D. (1970). A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology. 48 (3): 443–53
R Bellman, On the Theory of Dynamic Programming. Proceedings of the National Academy of Sciences, 1952
Smith, Temple F. & Waterman, Michael S. Identification of common molecular subsequences. Journal of Molecular Biology, volume 147, Issue 1, 25 March 1981, Pages 195-197. PDF
Stephen F. Altschul, Warren Gish, Webb Miller, Eugene W. Myers and David J. Lipman, Basic Local Alignment Search Tool. J. Mol. Biol. 1990 Oct 5;215(3):403–10. https://blastalgorithm.com/
